1 + 2 + 3 + … = – 1/12 and Related Results
This post was written by my father, John Weaver, and originally published on October 15, 2015 on his blog: beorminga.wordpress.com. I am preserving them on my website as his blog posts are remarkable in their thoroughness and depth of research. Enjoy!
1 + 2 + 3 + … = – 1/12 and Related Results
The seemingly bizarre result in the title of this article has surprisingly found its way into some branches of advanced physics including string theory. Its ‘proof ‘ is demonstrated in one of the Numberphile videos on YouTube where divergent series are manipulated in an easy-going manner, along the following lines:
T = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + …
Add zero
T = 0 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − …
hence
2T = 1 + 0 + 0 + 0 + 0 + 0 + 0 + … = 1, ⇒ T = ½
Similarly
U = 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + …
U = 0 + 1 − 2 + 3 − 4 + 5 − 6 + 7 − …
2U = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + … = T = ½, ⇒ U = ¼
S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + …
U = 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + …
S − U = 2(2 + 4 + 6 + 8 + … ) = 4(1 + 2 + 3 + 4 + … ) = 4S, ⇒ 3S = − U = − ¼
whence S = − 1/12. Mathematically this result can be recognised as an expression of the Riemann zeta function ζ(z) evaluated at z = − 1.
It occurred to me that it should also be possible to sum powers of the natural numbers using the same carefree operations on divergent series as in the Numberphile video. In the linked discussion Some Fun with Divergent Series, I first evaluate the sum of the squares of the natural numbers S2 and then, after a digression on Abel summation and the Riemann zeta function, I generalise the method to find the sum Sn of the series of natural numbers raised to the nth power. Initially a recursion relation is found for a related quantity Tn , the sum of powers of the natural numbers with alternating signs. This leads directly to the formula for Sn and its connection with the well-known Bernoulli numbers.
After completing this articleI discovered a WordPress blog by the eminent Australian/American mathematician Terry Tao. In one of his published articles there, entitled The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation, he explores the summation of powers of the natural numbers in much greater detail and, of course, with considerably more insight than anything I could offer. Nevertheless I have kept my approach posted here as it is a natural generalisation of the informal method shown in the Numberfile video referred to above.

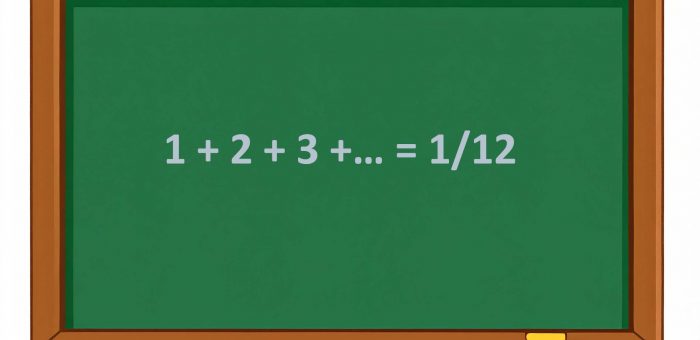



Leave A Comment